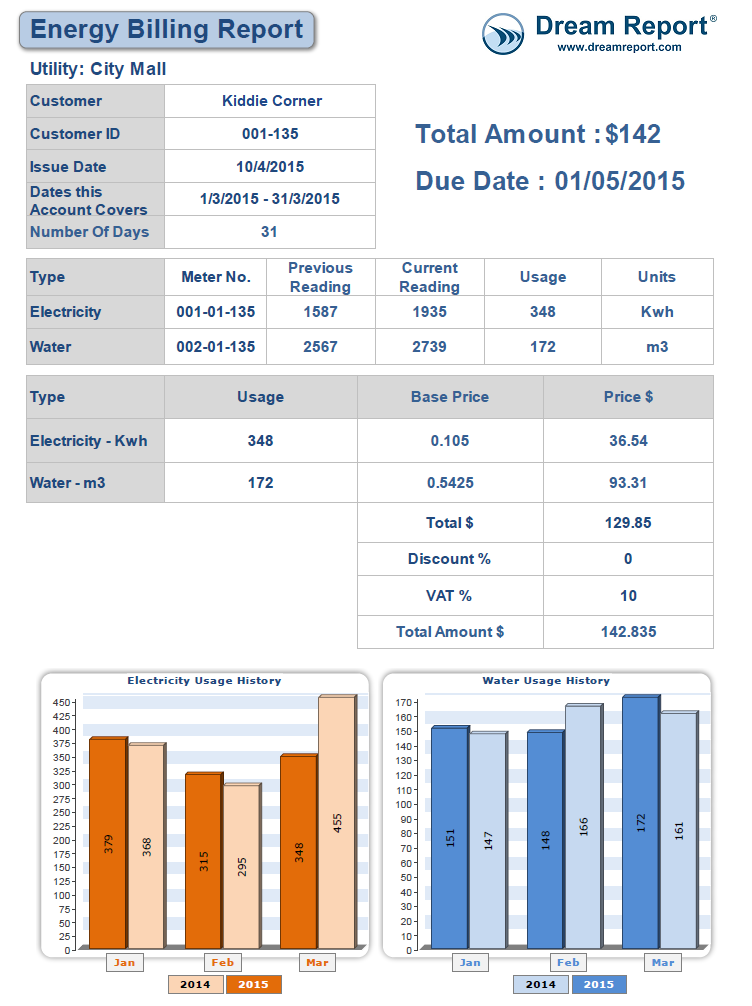
Calculator Use
Calculate basic summary statistics for a sample or population data set including minimum, maximum, range, sum, count, mean, median, mode, standard deviation and variance.
Enter data separated by commas or spaces.
You can also copy and paste lines of data from spreadsheets or text documents. See all allowable formats in the table below.
Power (1 – Beta) is not considered in these calculations. Power and Sample Size may be calculated using SigmaXL Statistical Tools Power & Sample Size Calculators. This sample size calculator is based on a confidence interval approach, where you enter the desired half-interval value (delta). The dice probability calculator is a great tool if you want to estimate the dice roll probability over numerous variants. There are may different polyhedral die included, so you can explore the probability of a 20 sided die as well as that of a regular cubic die. There are 7 calculators in this category. Descriptive Statistics Calculator - Find Arithmetic mean, mode, median, minimum, maximum of a data set. Standard Deviation Calculator - Find standard deviation, variance and range of a data set. Probability Calculator - Finds conditional probability, union and intersection of events.
Basic Statistics Calculations for this Calculator
Below is a listing of the statistical values calculated and the formulas used by this calculator. Values in a set of data are represented by x1, x2, x3, ... xn.
How to Find the Minimum
Ordering a data set from lowest to highest value, x1 ≤ x2 ≤ x3 ≤ ... ≤ xn, the minimum is the smallest value in the data set, x1. The formula for minimum is:
[ text{Min} = x_1 = text{min}(x_i)_{i=1}^{n} ]How to Find the Maximum
Ordering a data set from lowest to highest value, x1 ≤ x2 ≤ x3 ≤ ... ≤ xn, the maximum is the largest value in the data set, xn. The formula for maximum is:
 [ text{Max} = x_n = text{max}(x_i)_{i=1}^{n} ]
[ text{Max} = x_n = text{max}(x_i)_{i=1}^{n} ] How to Find the Range
The range of a data set is the difference between the minimum and maximum. To find the range, calculate xn minus x1.
[ R = x_n - x_1 ]How to Find the Sum
The sum is the total of all data values added together, x1 + x2 + x3 + ... + xn. The formula for sum is:
 [ text{Sum} = sum_{i=1}^{n}x_i ]
[ text{Sum} = sum_{i=1}^{n}x_i ] How to Find the Count: What is the Size of a Data Set?
The count is the number of data values in a data set.
[ text{Count} = text{Size} = n = text{count}(x_i)_{i=1}^{n} ]How to Calculate the Mean
The mean is the sum of all of the data values divided by the size of the data set. The mean is also known as the average. To find the mean add all of the values and divide by the count. The only difference between a sample mean and a population mean is the symbol used to express the mean.
For a Population
[ mu = dfrac{sum_{i=1}^{n}x_i}{n} ]For a Sample
[ overline{x} = dfrac{sum_{i=1}^{n}x_i}{n} ]How to Find the Median
Easy Statistics Calculator
Ordering a data set from lowest to highest value, x1 ≤ x2 ≤ x3 ≤ ... ≤ xn, the median is the value separating the upper half of the ordered data from the lower half. If n is odd the median is the center value. If n is even the median is the average of the 2 center values.
If n is odd the median is the value at position p where
[ p = dfrac{n + 1}{2} ] [ widetilde{x} = x_p ]If n is even the median is the average of the values at positions p and p + 1 where
[ p = dfrac{n}{2} ] [ widetilde{x} = dfrac{x_{p} + x_{p+1}}{2} ]How to Find the Mode
The mode is the value or values that occur most frequently in the data set. Count the number of times each value in a data set occurs. The mode is the data value with the highest count.
How to Calculate Standard Deviation
Standard deviation is a measure of dispersion of data values about the mean. The formula for standard deviation is the square root of the sum of squared differences from the mean divided by the size of the data set.
For a Population
[ sigma = sqrt{dfrac{sum_{i=1}^{n}(x_i - mu)^{2}}{n}} ]For a Sample
[ s = sqrt{dfrac{sum_{i=1}^{n}(x_i - overline{x})^{2}}{n - 1}} ]How to Calculate Variance
Variance measures dispersion of data from the mean. The formula for variance is the sum of squared differences from the mean divided by the size of the data set.
For a Population
[ sigma^{2} = dfrac{sum_{i=1}^{n}(x_i - mu)^{2}}{n} ]For a Sample
[ s^{2} = dfrac{sum_{i=1}^{n}(x_i - overline{x})^{2}}{n - 1} ]Options
54
65
47
59
40
53
54,
65,
47,
59,
40,
53,
or
42, 54, 65, 47, 59, 40, 53
65 47
59 40
53
or
42 54 65 47 59 40 53
54 65, 47,59,
40 53
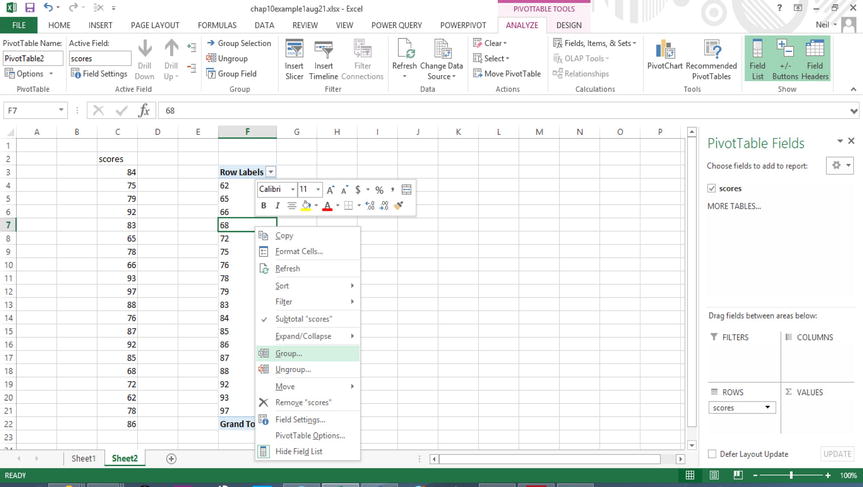
Statistical Calculator App
See Descriptive Statistics Calculator for more advanced statistics calculations.
